Anleitung

1. Markiere einen Mittelpunkt \(M\). Ziehe um \(M\) einen Kreis \(k\) mit beliebigem Radius. Dieser Kreis wird später der Umkreis des Fünfecks sein.
   
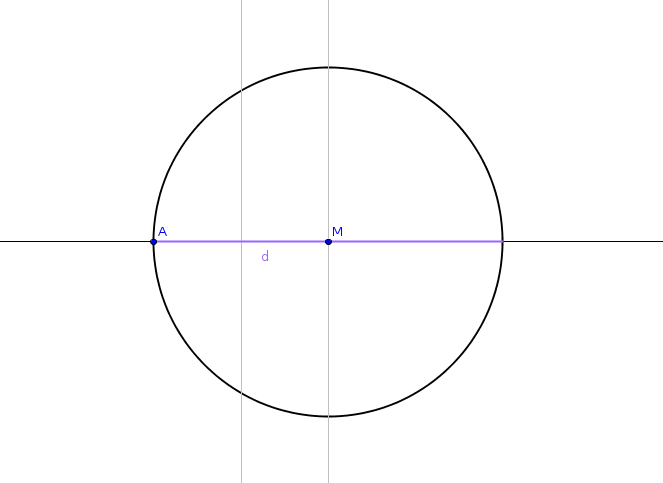
2. Zeichne einen Durchmesser \(d\) zum Umkreis, also eine Sehne, die durch den Mittelpunkt verläuft. Die Schnittpunkte von \(d\) mit dem Kreis \(k\) sollen \(A\) und \(B\) heißen.
3. Konstruiere eine Senkrechte \(s\) zu \(d\) durch den Mittelpunkt \(M\). Markiere den Schnittpunkt \(S\) von \(s\) mit \(k\).
4. Konstruiere den Mittelpunkt der Strecke \([AM]\). Bezeichne diesen Mittelpunkt mit \(N\).
5. Trage die Streckenlänge \(\overline{NS}\) auf \(d\) von \(N\) aus ab. Der Endpunkt dieser Strecke sei \(E\). (Kreisbogen um \(N\) mit Radius \(\overline{NS}\))
   
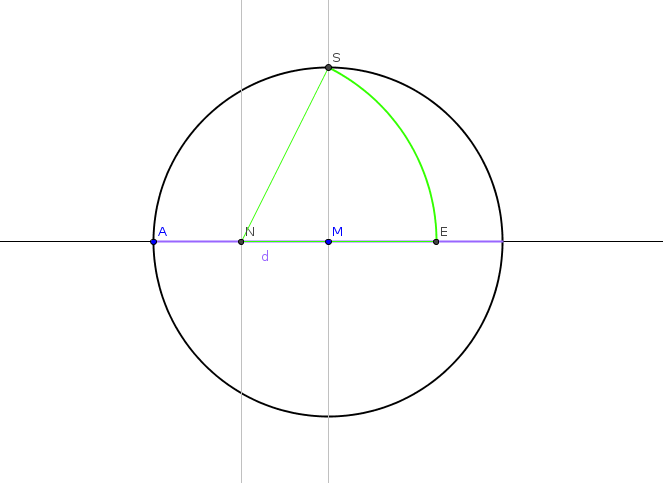
6. Die Streckenlänge \(\overline{SE}\) ist die gesuchte Kantenlänge des Fünfecks. Trage diese beginnend bei \(S\) auf dem Kreis \(k\) so oft ab, bis alle Eckpunkte des Fünfecks markiert sind.
   
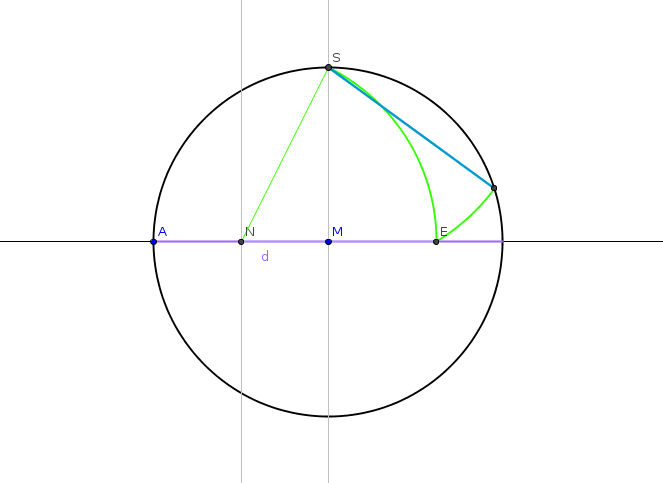
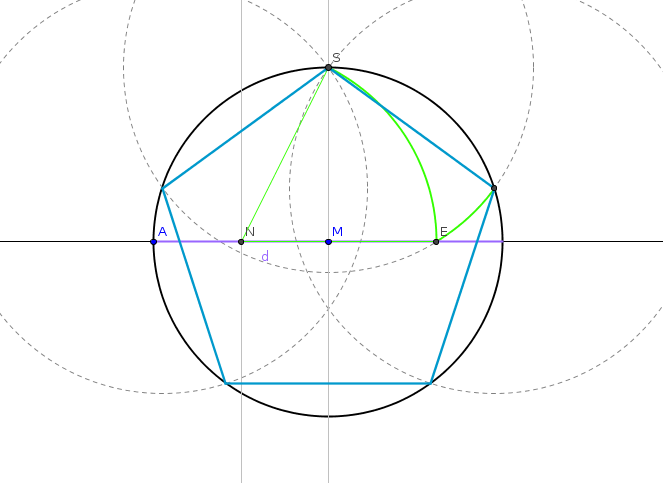
7. Zeichne das Fünfeck.