Näherungskonstruktion eines regelmäßigen Siebenecks
Abschlussbedingungen
Anzeigen
Näherungskonstruktion 7-Eck
- Zeichne um einen Punkt \( A \) einen Kreis \( k \) mit Radius \( r \). Markiere einen Punkt \( B \) auf \( k \). \( k \) wird der Umkreis des Siebenecks sein.
- Zeichne auch um \( B \) den Kreis mit Radius \( r \).
- Markiere einen der beiden Schnittpunkte der beiden Kreise als Punkt \( C \). Zeichne das Dreieck \( ABC \). \( \triangle ABC \) ist gleichseitig.
- Zeichne die Höhe durch den Punkt \( C \) im Dreieck \( ABC \) ein. Der Höhenfußpunkt ist \( D \).
- Zeichne um \( C \) den Kreis \( m \) mit Radius \( \overline{CD} \).
- Bezeichne die Schnittpunkte von \( m \) mit \( k \) als \( E \) und \( F \). Die Strecken \( [CE] \) und \( [CF] \) sind bereits näherungsweise zwei Seiten des Siebenecks.
- Vervollständige das Siebeneck durch schrittweises Abtragen von \( \overline{CE} \) auf der Kreislinie \( k \).
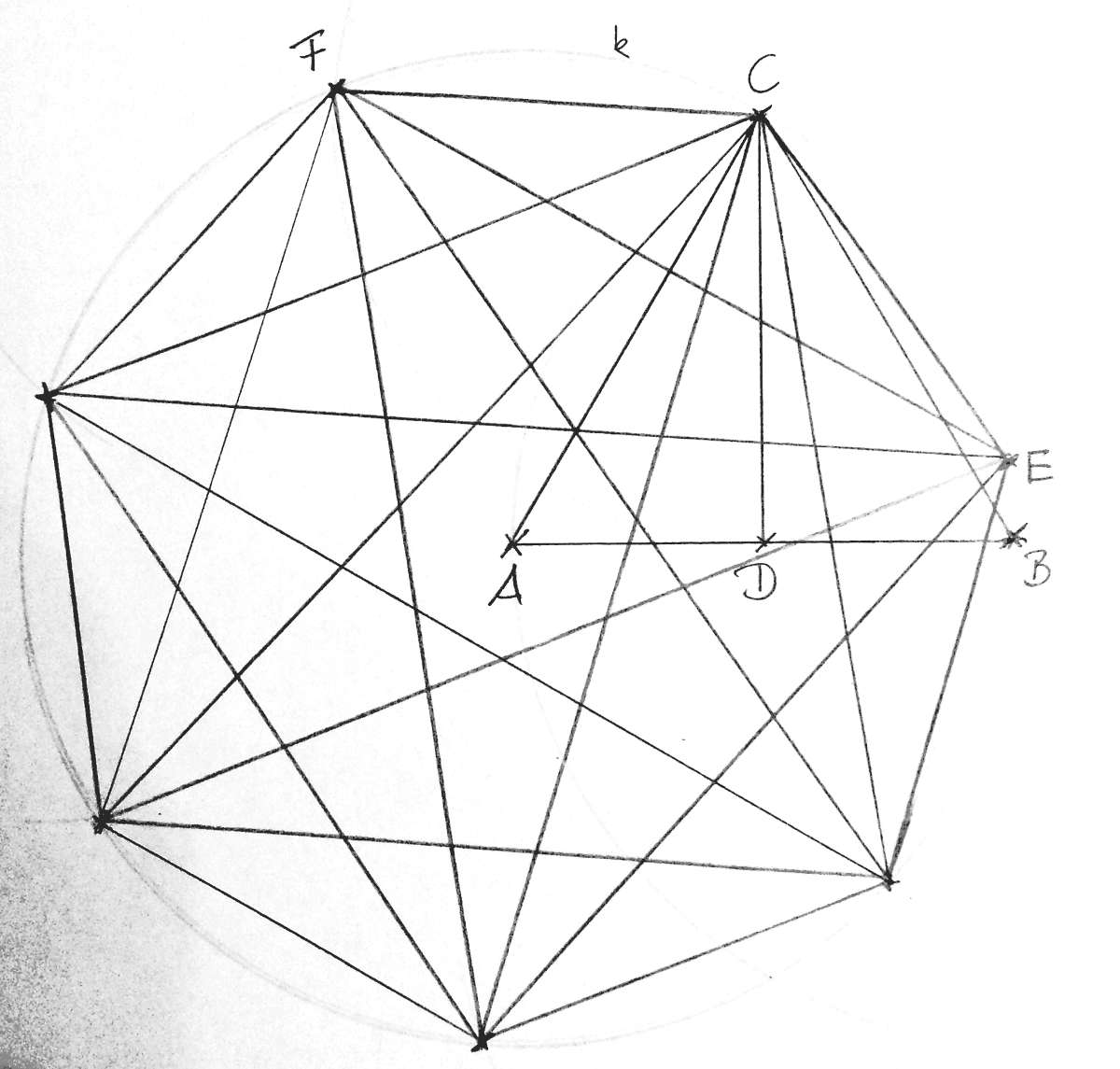
Zuletzt geändert: Donnerstag, 11. Februar 2016, 18:28