Näherungskonstruktion 9-Eck

(nach Albrecht Dürer 1525: "Underweysung der messung mit dem zirckel un richtscheyt")

Im Original schreibt Dürer:

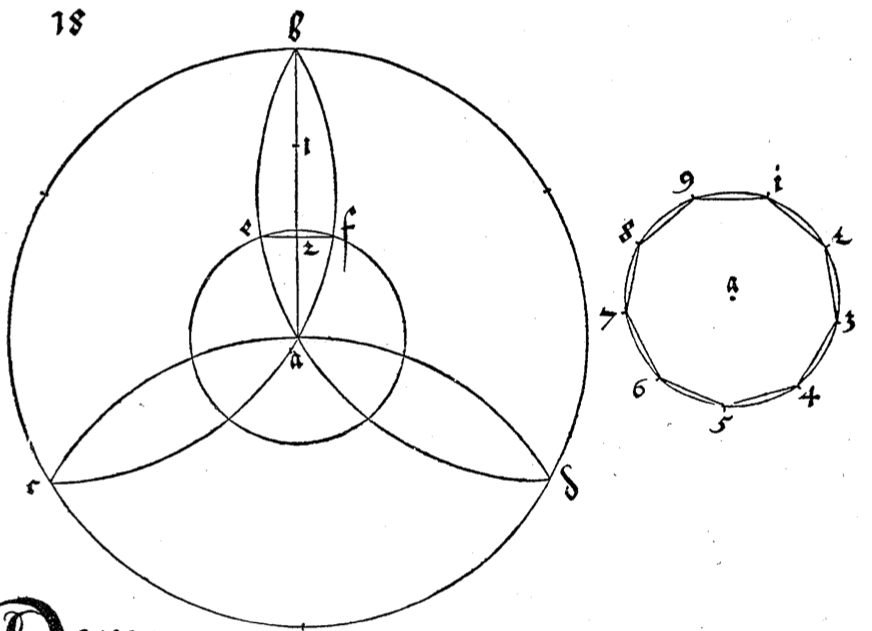
Ein neun eck ist durch ein dryangel zu finden/ also/ Reiß auß einem Centrum .a. ein grosse zirckellini/ darein reiß mit unuerrucktem zirckel/ drey fischs blosen/ der obern ende an der zirckellini sey .b. der andern end auf den seyten sey .c.d. Darnach reiß in der obern fischblosen ein aufrechte gerade lini .b.a. dise lini teil mitzweyen punkte .1.2. in drey gleiche felt/ also das 2. der negst punckt beym .a. sey/ unnd far durch den punckten .2. mit einer geraden zwerch lini zu gleichen wincklen .b.a. und wo sie die blosen lini zubeden seyten durchschneidet/ da setz .e.f. Darnach nym ein zirckel/ setz in mit dem fuß/ in das Centru .a. undden andern in den punckten .e. und reiß durch das .f. zu ring herumb/ ein zirckellini so geet die leng .e.f. zuneun mal in disem zirckelriß herum/ solchs hab ich hernach aufgeryssen.

Da dieses mittelalterliche Fränkisch sich heute nicht mehr so leicht lesen lässt, jetzt nochmal in heutigem Deutsch:

1. Ein Neuneck lässt sich über ein Dreieck finden. Also beginne mit einem Punkt \( a \) und zeichne um diesen Punkt einen großen Kreis mit Radius \( r \).
2. Zeichne in diesen Kreis drei Fischblasen. D.h. trage den Radius \( r \) des Kreises auf seiner Kreislinie so oft wie möglich ab. Dann ziehe um jeden zweiten der so gefundenen Punkte einen Kreis wiederum mit Radius \( r \).
3. Die drei Spitzen der Fischblasen werden nacheinander mit \( b \), \( c \) und \( d \) bezeichnet.
4. Zeichne die Strecke von \( a \) nach \( b \). Teile diese Strecke in drei gleich lange Teile. Der innere Teilpunkt wird mit \( 2 \) bezeichnet, der äußere mit \( 1 \).
5. Errichte die Senkrechte zur Strecke durch \( a \) und \( b \) durch den Teilpunkt \( 2 \).
6. Die Schnittpunkte dieser Senkrechten mit der Fischblase, die durch \( b \) gegeben ist, werden mit \( e \) und \( f \) bezeichnet.
7. Zeichne die Geraden durch \( a \) und \( e \), sowie durch \( a \) und \( f \) ein. Die Schnittpunkte dieser Geraden mit dem großen Kreis sind die ersten beiden Punkte des Neunecks.
8. Trage die Seitenlänge des Neunecks so oft auf dem großen Kreis ab, bis alle neun Eckpunkte gefunden sind.
9. Zeichne das Neuneck.