Topic 4

Ströme und Leistungen in Abhängigkeit von der Spannung

Auch hier wird für die Simulation der Innenwidestand R₁ als konstant angenommen diesmal aber die Spannung U schrittweise verändert.


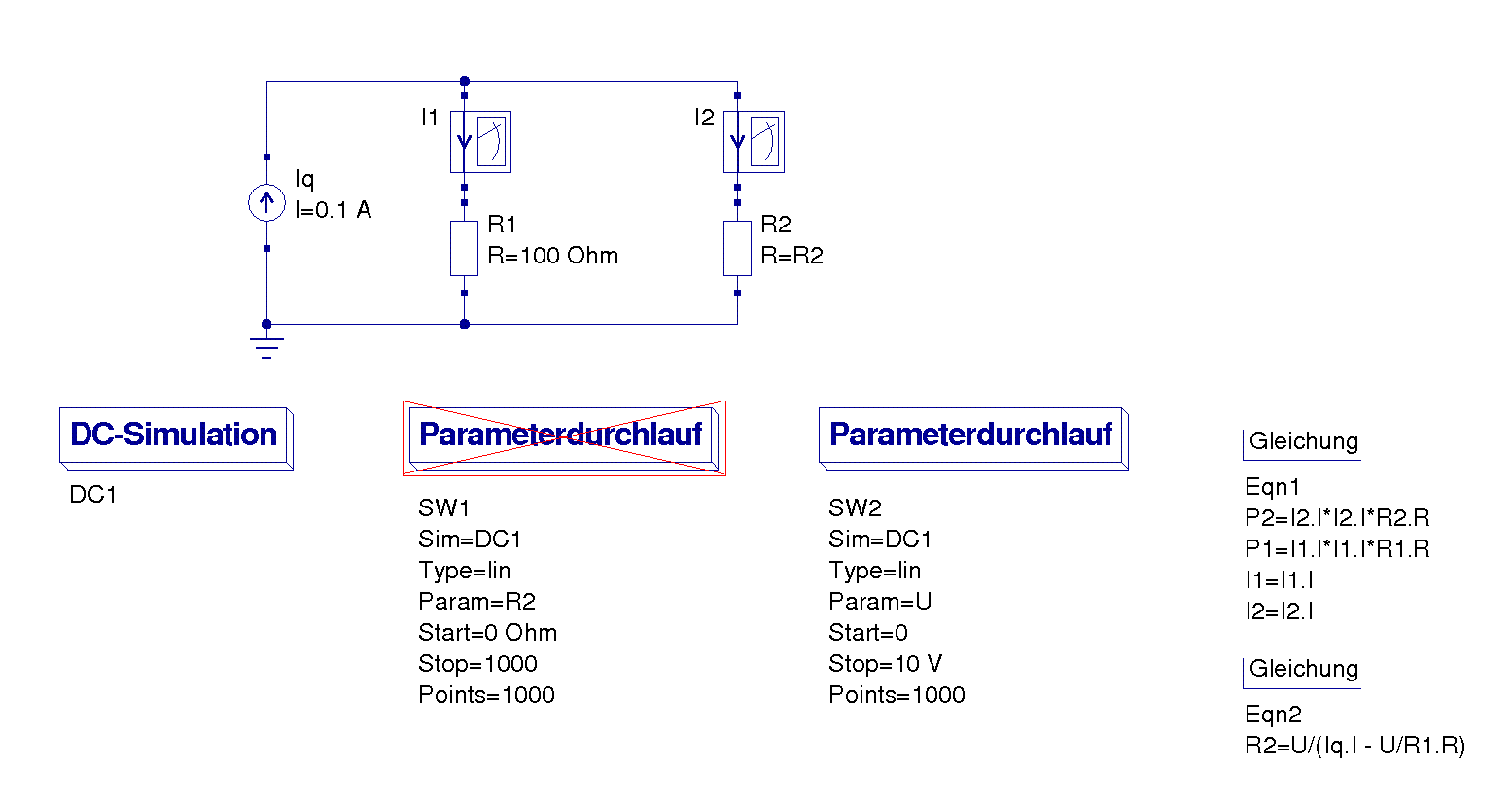
Da die Spannung in der Simulation nicht direkt änderbar ist (es wird ja eine Stromquelle genutzt), läßt sich eine Spannungsänderung nur über eine Änderung des Widerstandes R₂ erreichen. Für den Widerstand R₂ ergibt sich: R₂ = U/(I_q - U/R₁)
Die Leistungen berechnen sich wie bereits oben angegeben.


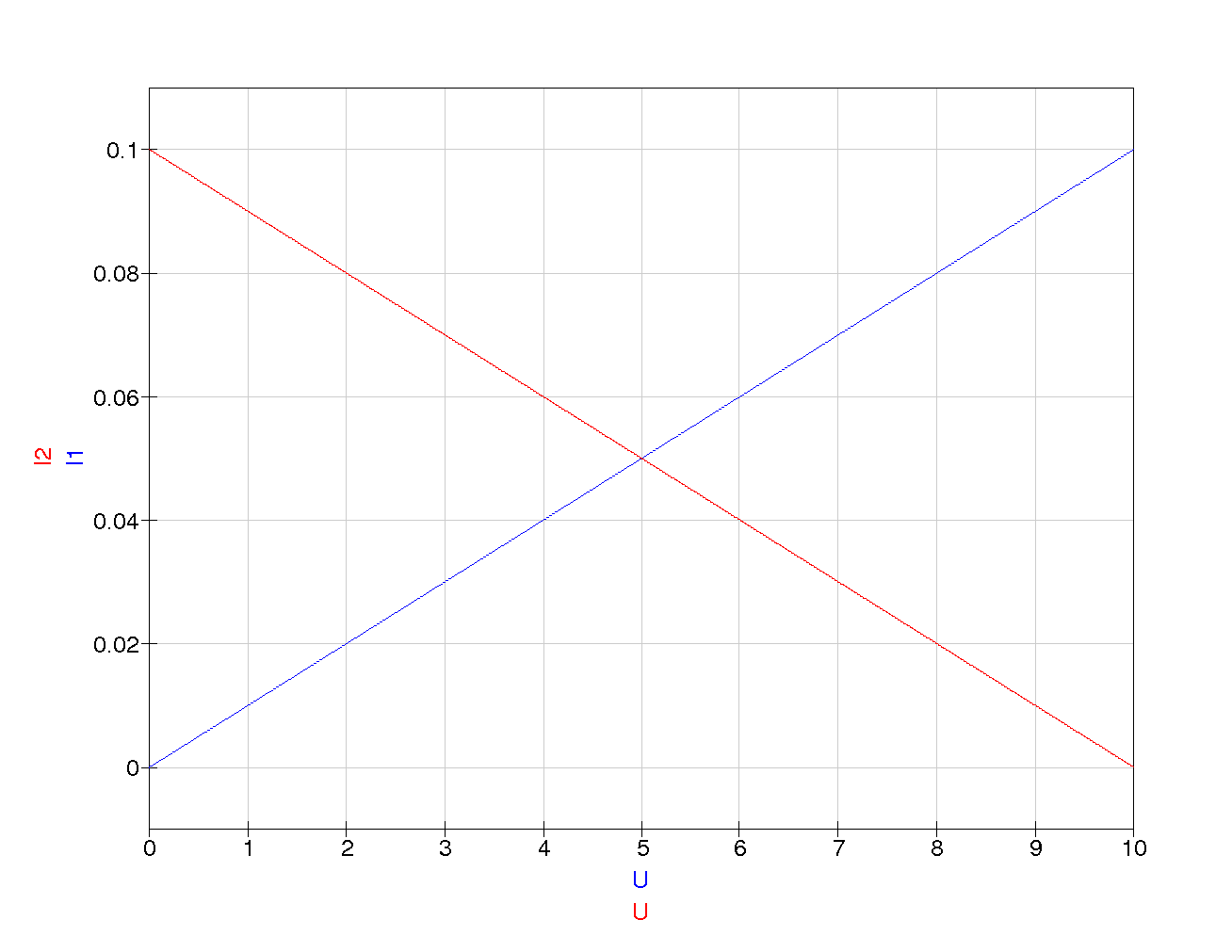
I1 und I2 sind die Ströme durch die Widerstände R₁ bzw. R₂.
Auch hier gilt, dass die Summe der beiden Ströme immer konstant und gleich dem Quellstrom ist: I_q = I₁ + I₂
Der Anstieg des blauen Graphen I1(U) entspricht dem Innenleitwert 1/R₁.
Der Schnittpunkt des roten Graphen I2(U) mit der x-Achse entspricht dem Leerlauf, d.h. es fließt kein Strom (I=0) und U ist maximal und entspricht der Leerlauf- bzw. Quellspannung.
Der Schnittpunkt des roten Graphen I2(U) mit der y-Achse entspricht dem Kurzschluß, d.h. die Spannung U = 0, der fließende Strom ist der Quellstrom I_q. Es gilt: I_q = I_K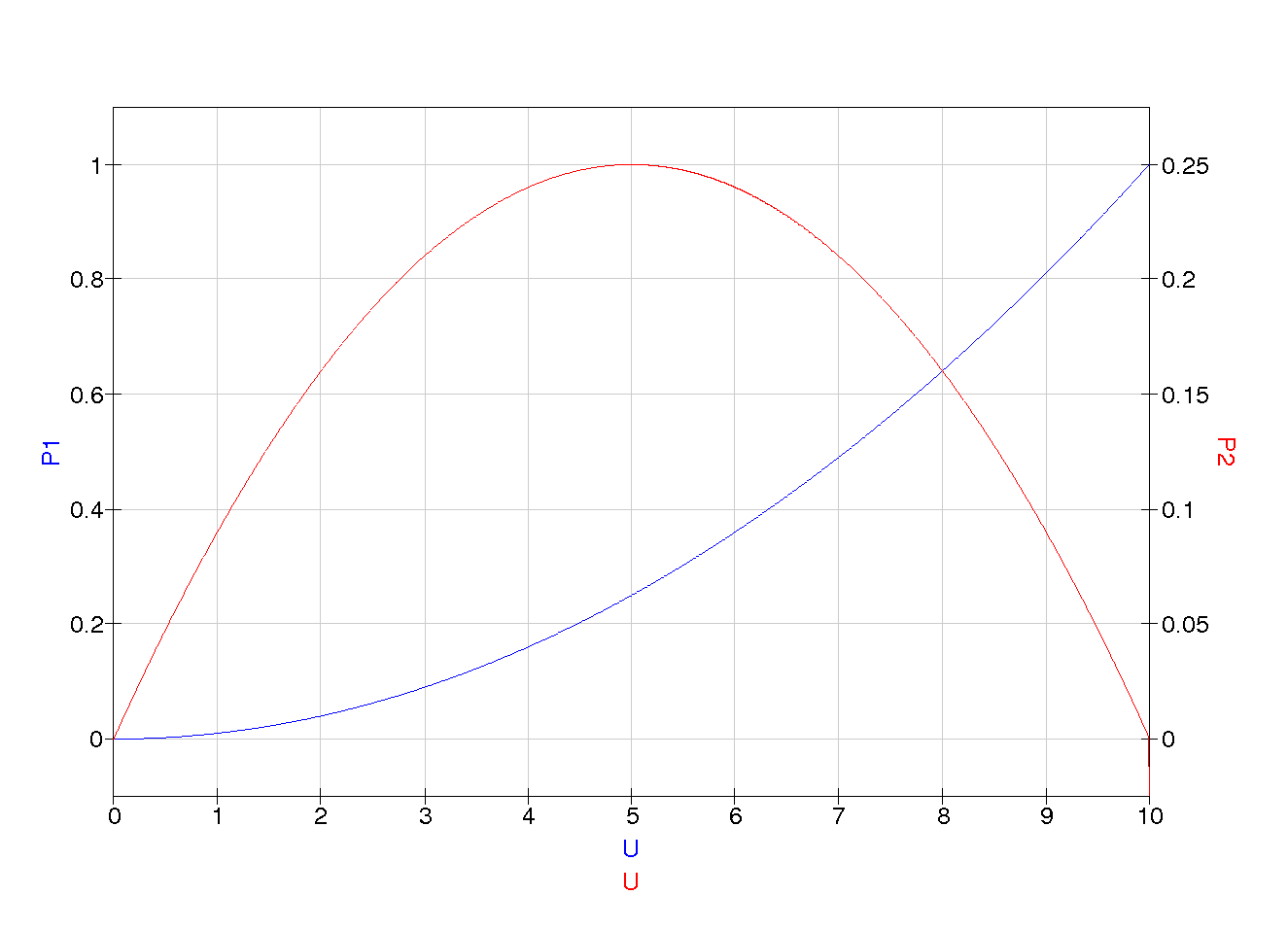


P1 und P2 sind die Leistungen an den Widerständen R₁ bzw. R₂.
Aus dem Diagramm ist zu erkennen, dass die Leistung am Widerstand R₂ an der Stelle U = U_q/2 ihr Maximum erreicht. Die Leistung am Innenwiderstand R₁ wird bei U = U_q maximal.
Es gilt: P₁ = P₂ bei U = U_q/2

Desweiteren ist aus den Diagrammen zu erkennen, dass das Leistungsmaximum von P₂ immer mit dem halben Kurzschlußstrom, der halben Quellspannung sowie gleichen Widerständen und damit der Leistungsanpassung zusammenfällt.
Es gilt: P_2max = U_q*I_q/4 bei U = U_q/2, I = I_q/2 und R₁ = R₂